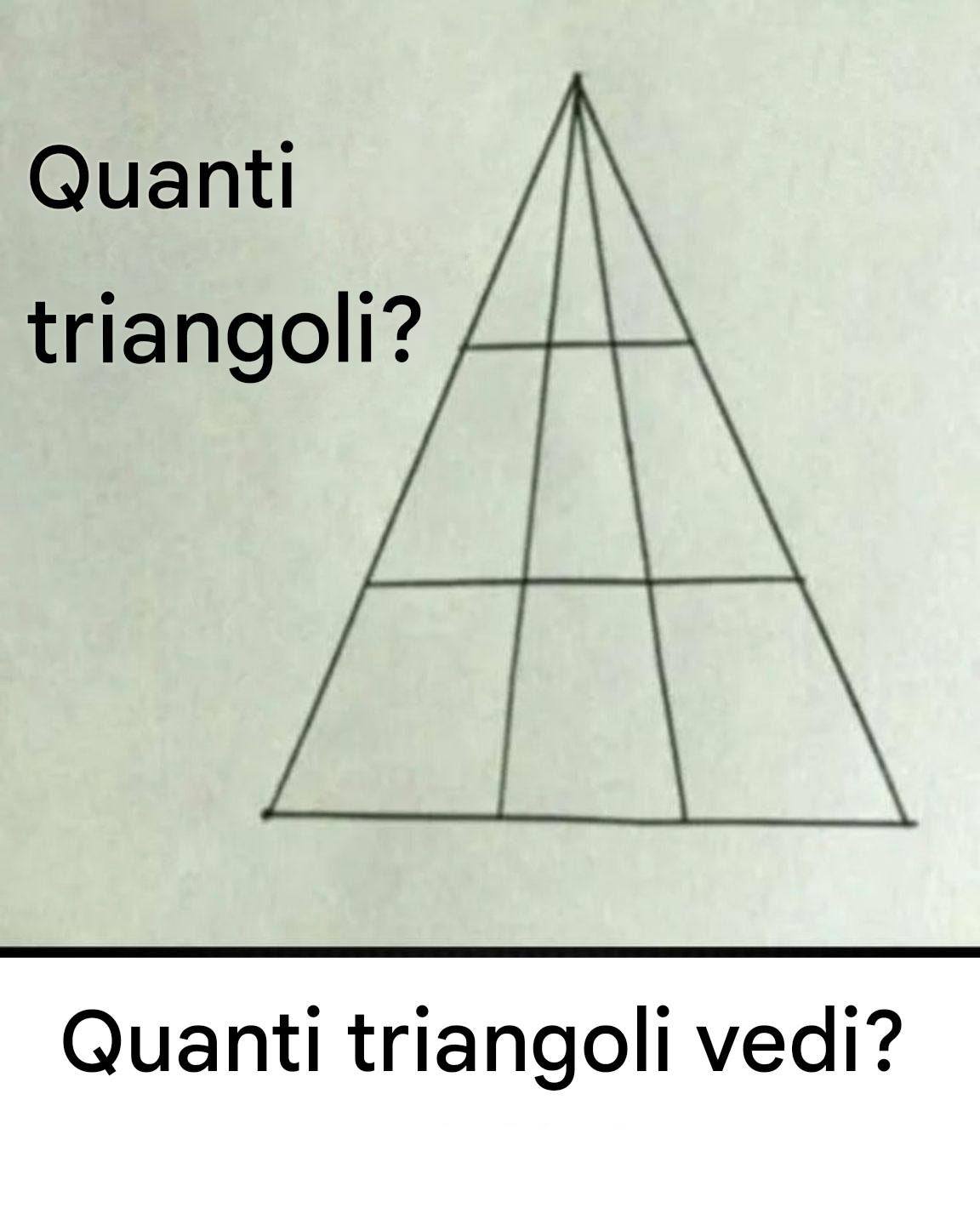
Quanti triangoli vedi in questa immagine?
Pensavi di aver trovato la risposta giusta, ma… questo famoso rompicapo ha lasciato indifferenti più di un occhio esperto! A prima vista, si contano alcuni triangoli, poi si sommano man mano che si avanza nei « livelli ». Semplice? Non proprio. La figura – un grande triangolo tagliato alla base da tre linee parallele – nasconde più forme di quante si possano immaginare. Pronti a evitare la trappola e a brillare al prossimo quiz aperitivo? Seguite la guida.
La trappola dei triangoli nascosti
Il nostro cervello ama individuare i triangoli piccoli e ovvi e… dimenticare quelli grandi che si formano combinando diverse aree. Di conseguenza, sottovalutiamo. Nella configurazione classica (4 file formate da 3 linee parallele alla base), la risposta corretta è 27. Se
avessi indovinato 26, molto probabilmente ti sarebbe sfuggito un grande triangolo composto, spesso un triangolo con la punta rivolta verso l’alto che si estende su 3 livelli, o un triangolo « mezzo largo » su un lato.
Metodo passo dopo passo: contare senza sbagliare

Altezza 1 livello: 10
Altezza 2 livelli: 6
Altezza 3 livelli: 3
Altezza 4 livelli: 1
Subtotale “su”: 10 + 6 + 3 + 1 = 20.
Aggiungere i triangoli “rivolti verso il basso” risultanti dall’annidamento dei segmenti: 7.
Totale: 20 + 7 = 27.
Consiglio mnemonico: pensa “20 in alto + 7 in basso” ed eviterai la classica dimenticanza.
La formula magica spiegata in modo semplice

Volete una scorciatoia elegante? Per un triangolo grande suddiviso in n righe da linee parallele alla base (qui n = 4), possiamo usare la seguente formula:
T(n) = n × (n + 2) × (2n + 1) ÷ 8
Applicato a n = 4:
T = 4 × 6 × 9 ÷ 8 = 27
⏬️⏬️ Continua nella pagina successiva ⏬️⏬️